John Walk
ELMy H-Mode Modeling (doctoral thesis)
John Walk
The ELMy H-mode is the most commonly-accessed high-performance regime on major tokamak experiments. The bursts of energy and particle transport driven by ELM crashes provide sufficient venting of impurities to allow stationary operation without excessive radiative losses - as such, it is considered the baseline scenario for reactor operation. However, on reactor-scale devices, ELMs drive pulsed heat loading unacceptable levels of erosion and damage to plasma-facing materials.
As a component of my doctoral research, I implemented an experimental and computational study of the pedestal in ELMy H-mode, necessary to the understanding and prediction of H-mode baseline operation on reactor-scale tokamaks (since the ELM stability limit is an important upper bound on tokamak operation). My work was featured in the 2011 DOE Joint Research Target, a nationally-coordinated research effort focusing on predictive modeling capability - the data from my analysis on MIT’s Alcator C-Mod experiment represents the world-record thermal pressure and magnetic field in a tokamak, and is unique in reaching comparable magnetic fields and thermal pressures targeted for the reactor-scale ITER device.
This study focused on the theory underlying the EPED model [1] developed by P.B. Snyder, which describes the ELM stability limit by the instersection of two physics constraints – that the pedestal is defined first by width-limiting turbulence (dubbed the “kinetic-ballooning mode”), subsequently growing in height until a magnetohydrodynamic stability limit (the “peeling-ballooning limit”) is reached.
Experimentally, Pedestal parameters scale consistently with theoretical predictions - the pedestal width is consistently predicted by the KBM limit (width scaling with the square-root of normalized pressure, shown below, with a scale factor consistent with results on other standard tokamaks):

Similarly, the pressure pedestal height is consistent with both KBM and peeling-ballooning limitations - that is, assuming the pressure pedestal height is approximated by the width times the pressure gradient. The width trends with the square-root of the pressure (as above, for the KBM limit) and the pressure gradient is set by the plasma current Ip (predicted by peeling-ballooning theory). As a spot check, the pedestal height is checked against an alternate theory predicting the width scaling with the square root of the temperature, rather than pressure - the trend is still somewhat present due to covariance between temperature and pressure, but the prediction is decidedly poorer.
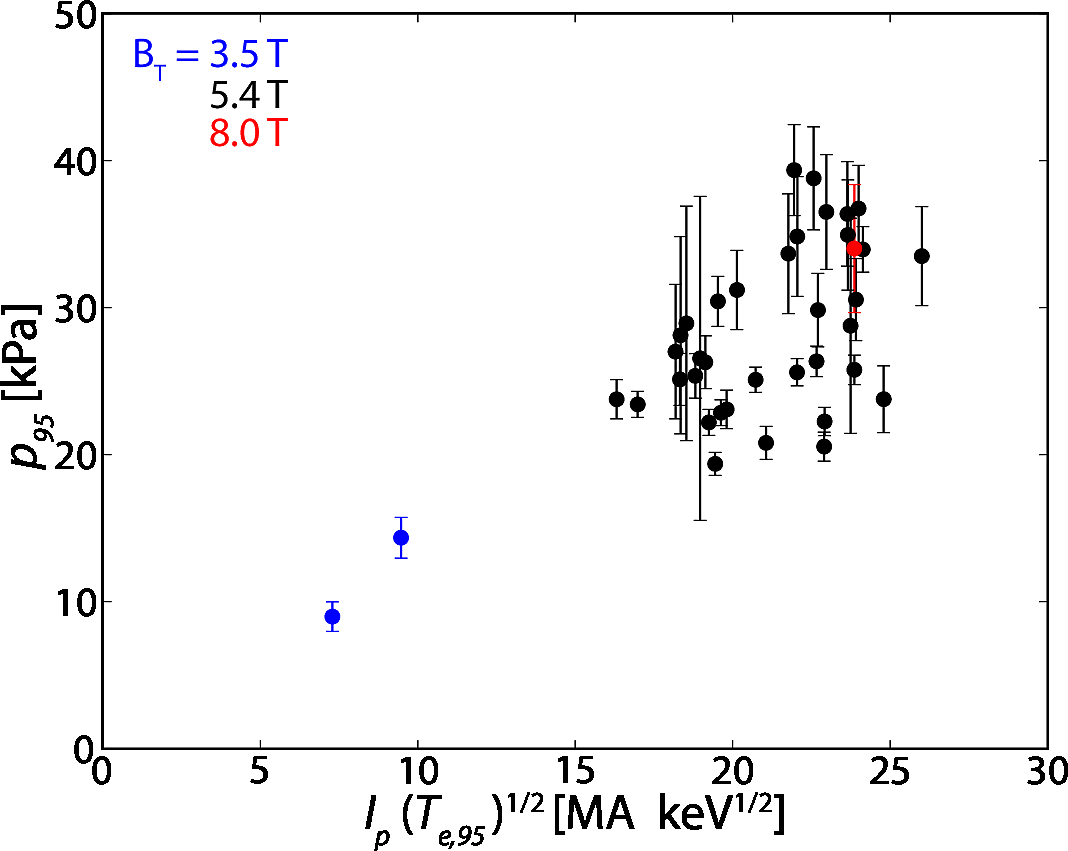
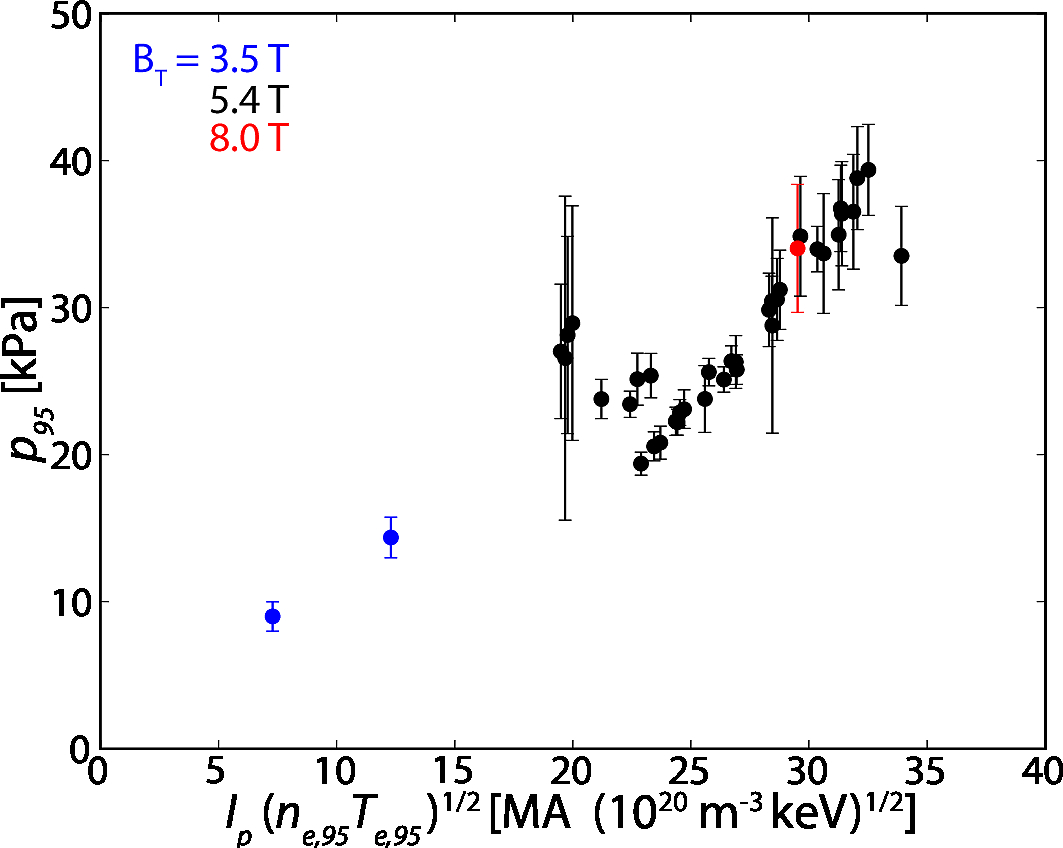
However, the dynamics of the pedestal are more complex than these trends can adequately capture, necessitating an integrated computational approach. I used the ELITE MHD stability code [2], which calculates the peeling-ballooning stability limit in terms of the drive terms (pedestal pressure gradient and electric-current density):
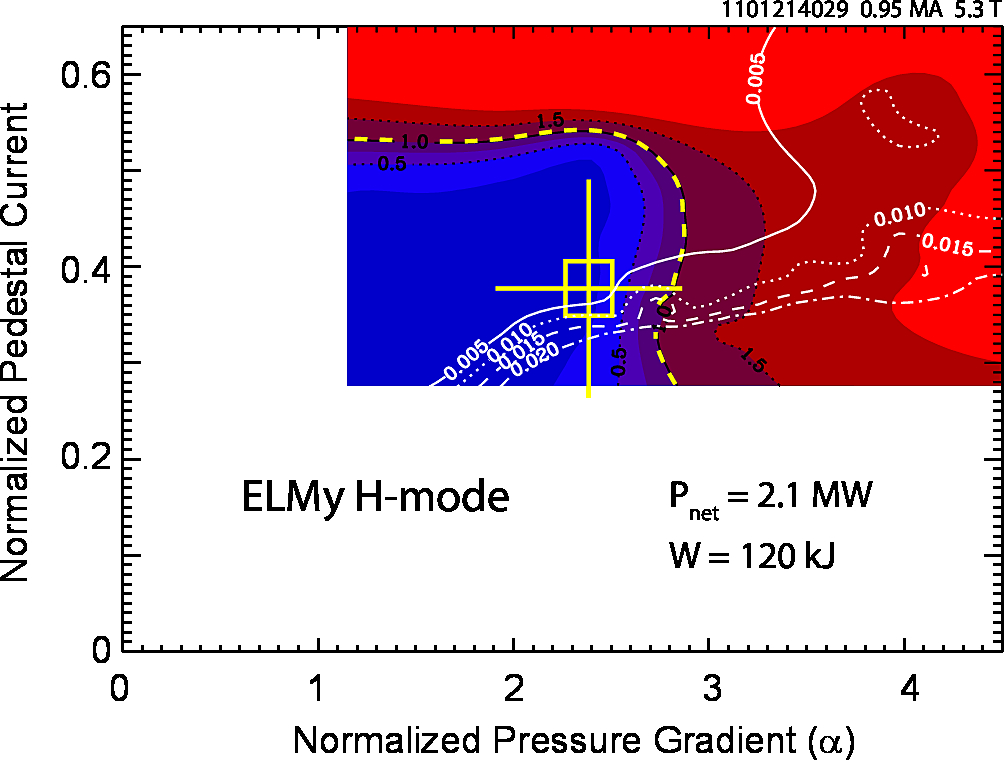
which computed the H-mode pedestal consistently to be at or near the peeling-ballooning stability boundary. Accordingly, EPED predictions based on these stability limits are consistently accurate (within the ~20% systematic uncertainty due to model simplifications) compared to the measured pedestal height - this represents a unique achievement in developing predictive capability for tokamak physics.
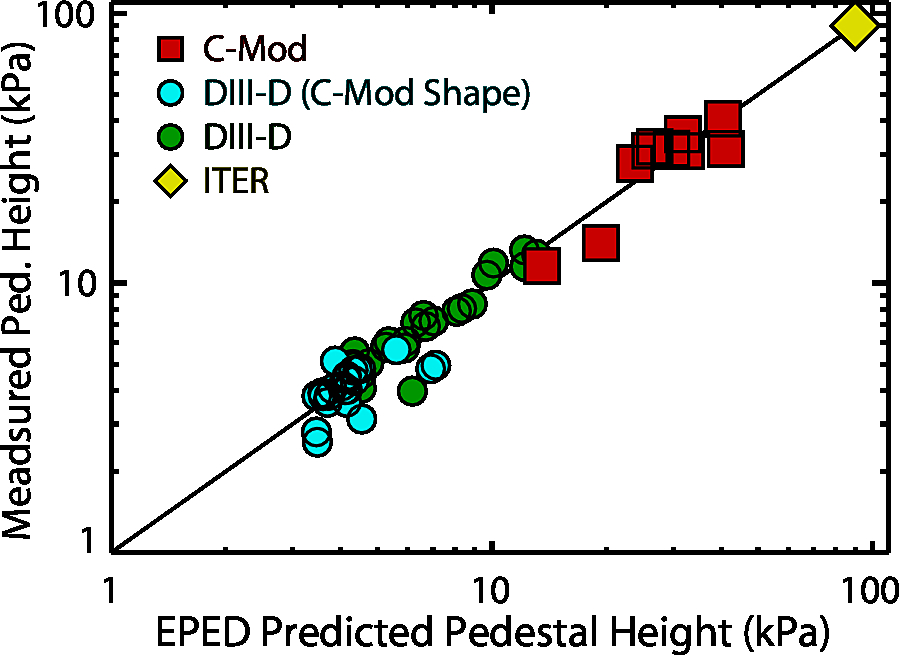
[1] P.B. Snyder, R.J. Groebner, A.W. Leonard, T.H. Osborne, and H.R. Wilson. Development and validation of a predictive model for the pedestal height. Physics of Plasmas, 16(5):056118, 2009.
[2] H.R. Wilson, P.B. Snyder, G.T.A. Huysmans, and R.L. Miller. Numerical studies of edge localized instabilities in tokamaks. Physics of Plasmas, 9(4):1277-1286, 2002.